Lorentz Transformation Tensor
The Roman indices i j k -. Here c is the speed of light which has the value c 299792458ms 1 Meanwhile is the ubiquitous factor s 1 1 2v c2 52 The Lorentz transformation 51encodeswithinitallofthefunideasoftimedilation.
The Lorentz transformation is xaLa bx baa.

Lorentz transformation tensor
. Some tensors with a physical interpretation are listed below. They cannot be parts of a vector. X x 6. First we have to suppose that there is a scalar potential and a vector potential that together make a four-vector.1 Laws of physics must be written a scalers vectors or tensors. The Electric and Magnetic fields are part of a rank 2 tensor and so they transform accordingly. In a static reference frame the four-velocity is umuc0 let me assume one spatial dimension for simplicity so the energy is just. En relativité restreinte elles correspondent aux lois de changement de référentiel galiléen pour lesquelles les équations de la physique sont préservées et pour lesquelles la vitesse de la lumière demeure identique dans tous les.
A contravariant 4-vector is an object defined as x x0. A flashbulb goes off at the origins when t 0. 3 Since the transformations mix together r and t it is pro table to devise a method to describe. The appropriate Lorentz transformation equations for the location vector are then r r t v.
2b or r r 1r vv tv. The Lorentz transformation is the linear relation 3. 2 Scalars vectors and tensors are defined by their transformation properties. They are called inertial or Galilean reference frames.
B x Bx B y By vEz 1 v2 B z Bz vEy 1 v2. X x - The Lorentz transformation tensor Λ transforms the spacetime coordinates x in frame K to the corresponding coordinates x in frame K. C 1 E x Ex E y Ey vBz 1 v2 E z Ez vBy 1 v2. A Lorentz tensor is by de nition an object whose indices transform like a tensor under Lorentz transformations.
X 0x 7x 0. If we boost to a frame in which the charge is moving there is an Electric and a Magnetic field. There are some elementary transformations in Lthat map one component into another and which have special names. According to postulate 2 the speed of light will be c in both systems and the wavefronts observed in both systems must be.
Since we could choose any direction for the axis that we boosted along these results for the field transformation are correct for all boosts. Indeed when you do a Lorentz boost your orientation changes and you cannot think of dV transforming as a simple length. For example a point charge at rest gives an Electric field. Another condition is that the speed of light must be independent of the reference frame in practice of the.
If one of the two events is at the origin x µ 1 0 the events light-like. In a different coordinate system the coordinates are xm. A Lorentz tensor is any quantity which transforms like a tensor under the homogeneous Lorentz transformation. Lorentz Transformations Our definition of a contravariant 4-vector in 1 whist easy to understand is not the whole story.
Lorentz Group Lorentz Invariant Lorentz Transformation REFERENCES. Coordinate systems are related by the Lorentz boost x0 x v c ct and ct0 ct v c x 51 while y0 y and z0 z. Otherwise inertial forces would appear. According to relativity no Galilean reference frame is privileged.
But since all events are subject to the same transformation the interval between two events s2 12 x1 x2x1 x2 is also invariant. Covariant Lorentz Transformation - With our geometry now defined we can write the Lorentz transformation in covariant notation as. X that transforms as a vector under Lorentz transformations. A 4-vector is a tensor with one index a rst rank tensor but in general we can construct objects with as many Lorentz indices as we like.
Ct x y z. You can walk up to the system choose your coordinate system and measure a particular component of the tensor in that coordinate system. - This can be represented in matrix notation as. I havent found it anywhere and I am slightly confused about tensors.
I know the tensor can be recognised by how it transforms but it feels strange that so important matrix is. The parity transformation P. You need to think of it as the component of a four-vector dVmuumu dV where umu is the four-velocity. Tensor the corresponding vector notation becomes hxyi xTgy.
The Lorentz transformation is independent of the state of the system but does depend on other data. In general the transformational nature of a Lorentz tensor clarification needed can be identified by its tensor order which is the number of free indices it has. Consider the space-time coordinates xm. What we mean by this precisely will be explained below.
The transformation of electric and magnetic fields under a Lorentz boost we established even before Einstein developed the theory of relativity. Derivation of Lorentz Transformations Use the fixed system K and the moving system K At t 0 the origins and axes of both systems are coincident with system Kmoving to the right along the x axis. These are the Lorentz transformations that are both proper det 1 and orthochronous 00 1. Principles and Applications of the General Theory of Relativity.
The Electromagnetic Field Tensor. Table 262 The Lorentz transformation of the electric and magnetic fields Note. The fundamental Lorentz transformations which we study are the restricted Lorentz group L. They cannot be parts of a vector.
Intervals can be positive space-like negative time-like or zero light-like. Les transformations de Lorentz sont des transformations linéaires des coordonnées dun point de lespace-temps de Minkowski à quatre dimensions. The matrix of the Lorentz transformation isnt a tensor because it switches the sign of the non-diagonal components during the inverse transformation right. Lorentz transformation Lessons from special relativity.
So it isnt basis independent but the Minkowski metrics is a tensor. Lorentz transformations consists of Lorentz transformation matrices for which 00 det 1 which is L 0 L L. As in the Galilean transformation the Lorentz transformation is linear since the relative velocity of the reference frames is constant as a vector. Note that the 4D tensor indices are denoted by Greek letters p v - - which take on the values 0 12 3 in our notation there are no imaginary is in the metric and no difference between zeroth and fourth components.
The time-reversal transformation T. Ct x y z. Do not include the time component. By construction Lorentz transformations leave the quantity x x x2 c2t2 invariant.
2a t t v rc2. No indices implies it is a scalar one implies that it is a vector etc. The equations in Table 262 tell us how E and B change if we go from one inertial frame to another. We know that E-fields can transform into B-fields and vice versa.
The Lorentz transformation isnt a function of the state of the system so its not meaningful to talk about measuring its components.
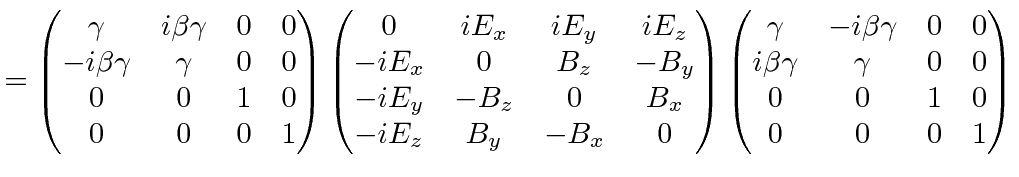
Lorentz Transformation Of The Fields
Einstein Relatively Easy The Lorentz Transformations Part Iv Lorentz Transformation Matrix

Solved 0 8 This One Is Tough The Electromagnetic Field Chegg Com
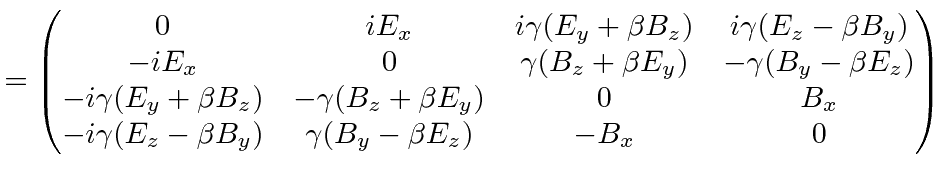
Lorentz Transformation Of The Fields

The General Lorentz Transformation Youtube

Lorentz Transformation In Matrix Form Lorentz Boost Special Theory Of Relativity Physics Youtube
Einstein Relatively Easy The Lorentz Transformations Part Iv Lorentz Transformation Matrix
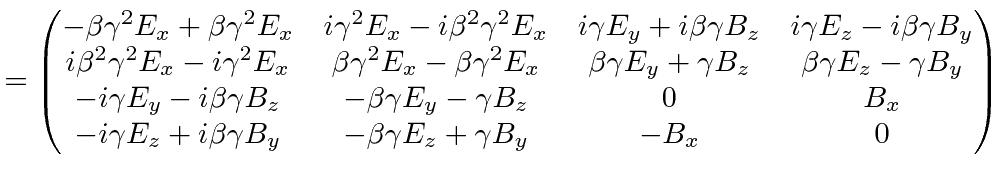
Posting Komentar untuk "Lorentz Transformation Tensor"